如图①，若点P是△ABC内或边上一点，且∠BPC=2∠A，则称点P是△ABC内∠A的二倍角点．请用直尺和圆规对图②、图③作出符合要求的点（保留作图痕迹，不写作法．）

0 返回出卷网首页

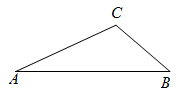
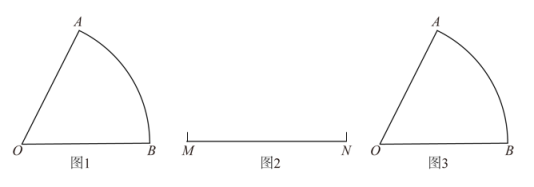
1. 如图①，若点P是△ABC内或边上一点，且∠BPC=2∠A，则称点P是△ABC内∠A的二倍角点．请用直尺和圆规对图②、图③作出符合要求的点（保留作图痕迹，不写作法．）

(1) 如图②，在△ABC内求作一点Q，使点Q是△ABC内∠A的一个二倍角点；

(2) 如图③，在△ABC外求作一点M，使点A是△MBC内∠M的一个二倍角点．

【考点】

圆周角定理; 尺规作图-垂直平分线;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 下面是小景设计的“过直线外一点作这条直线的垂线”的尺规作图过程．

已知：如图1，直线l和l外一点A ，

求作：直线 $\text{[math]}$ ，使得 $\text{[math]}$ 于点E ．

作法：①在直线l上取一点B ，连接 $\text{[math]}$ （如图2）；

②作线段 $\text{[math]}$ 的垂直平分线 $\text{[math]}$ ，交 $\text{[math]}$ 于点O；

③以O为圆心， $\text{[math]}$ 长为半径作圆，交直线l于点E；

④作直线 $\text{[math]}$ ．

所以直线 $\text{[math]}$ 即为所求作的直线．

(1) 使用直尺和圆规，补全图形（保留作图痕迹）；

(2) 完成下面的证明．

证明： $\text{[math]}$ 为线段 $\text{[math]}$ 的垂直平分线，

$\text{[math]}$

$\text{[math]}$ ．

$\text{[math]}$ 是 $\text{[math]}$ 的直径，

$\text{[math]}$ （）（填推理的依据）．

$\text{[math]}$ ．

综合题普通

2. 下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程．

已知： $\text{[math]}$ 中， $\text{[math]}$ ．

求作： $\text{[math]}$ ，使得 $\text{[math]}$ ．

作法：如图，

①分别以点 $\text{[math]}$ 和点 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧交于 $\text{[math]}$ 、 $\text{[math]}$ 点，作直线 $\text{[math]}$ ；

②分别以点 $\text{[math]}$ 和点 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧交于 $\text{[math]}$ 、 $\text{[math]}$ 点，作直线 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 交于点 $\text{[math]}$ ；

③连接 $\text{[math]}$ 和 $\text{[math]}$ ；

④以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 的长为半径作 $\text{[math]}$ ．

所以 $\text{[math]}$ ．

根据小菲设计的尺规作图过程．

(1) 使用直尺和圆规，补全图形（保留作图痕迹）；

(2) 完成下面的证明．

证明：连接 $\text{[math]}$

∵ $\text{[math]}$ 和 $\text{[math]}$ 分别为 $\text{[math]}$ 、 $\text{[math]}$ 的垂直平分线，

∴ $\text{[math]}$ ．

∴ $\text{[math]}$ 是 $\text{[math]}$ 的外接圆．

∵点 $\text{[math]}$ 是 $\text{[math]}$ 上的一点，

∴ $\text{[math]}$ ．（）．（填推理的依据）

综合题普通

3. 已知：如图，点M为锐角∠APB 的边PA上一点．

求作：∠AMD，使得点D在边PB上，且∠AMD ＝2∠P．

作法：

①以点M为圆心，MP长为半径画圆，交PA于另一点C，交PB于点D点；

②作射线MD．

(1) 使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2) 完成下面的证明．

证明：∵P、C、D都在⊙M 上，

∠P为弧CD所对的圆周角，∠CMD为弧CD所对的圆心角，

∴∠P＝ $\text{[math]}$ ∠CMD（）（填推理依据）．

∴∠AMD＝2∠P．

综合题普通