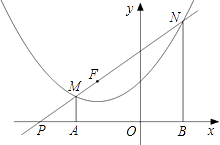
抛物线y= +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．

0 返回出卷网首页

1. 抛物线y= $\text{[math]}$ +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．

(1) 先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；

(2) 设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；

(3) 若射线NM交x轴于点P，且PA•PB= $\text{[math]}$ ，求点M的坐标．

【考点】

待定系数法求一次函数解析式; 待定系数法求反比例函数解析式; 反比例函数与一次函数的交点问题; 勾股定理; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平面直角坐标系xOy中，菱形ABCD的对角线AC与BD交于点P（-1，2），AB⊥x轴于点E，正比例函数y=mx的图像与反比例函数 $\text{[math]}$ 的图像相交于A，P两点。

(1) 求m，n的值与点A的坐标；

(2) 求证： $\text{[math]}$ ∽ $\text{[math]}$

(3) 求 $\text{[math]}$ 的值

综合题普通

2. 如图，在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 的图像与反比例函数 $\text{[math]}$ 的图像相交于 $\text{[math]}$ ， $\text{[math]}$ 两点．

(1) 求该反比例函数的表达式；

(2) 过点A作直线 $\text{[math]}$ ，交该反比例函数图象于另一点C，交y轴于点D、连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

3. 如图，一次函数y₁＝kx+b（k ， b为常数，k≠0）的图象与反比例函数y₂＝ $\text{[math]}$ （m为常数，m≠0）的图象相交于点M（1，4）和点N（4，n）．

(1) 反比例函数与一次函数的解析式．

(2) 函数y₂＝ $\text{[math]}$ 的图象（x＞0）上有一个动点C ，若先将直线MN平移使它过点C ，再绕点C旋转得到直线PQ ， PQ交x轴于点A ，交y轴点B ，若BC＝2CA ，求OA•OB的值．

综合题普通