1.
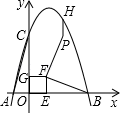
如图,在平面直角坐标系中, 的顶点E,F在x轴上,
的顶点E,F在x轴上, 且
且 , x轴上有两点
, x轴上有两点 ,
,  , 二次函数
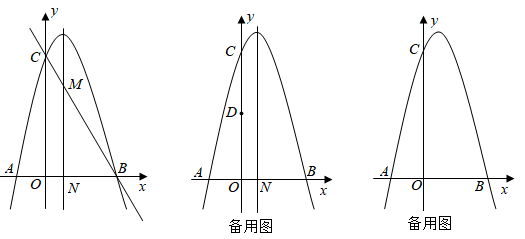
, 二次函数 的图象经过A、B两点,且与y轴正半轴交于点C,
的图象经过A、B两点,且与y轴正半轴交于点C, . 点
. 点 . 将
. 将 沿x轴向左平移,平移距离为
沿x轴向左平移,平移距离为 .
.

(1)
求a、b、c的值;
(2)
当点D首次落在抛物线上,求m的值;
(3)
当抛物线落在 内的部分,满足y随x的增大而增大时,请直接写出m的取值范围.
内的部分,满足y随x的增大而增大时,请直接写出m的取值范围.
【考点】
待定系数法求二次函数解析式;