1.
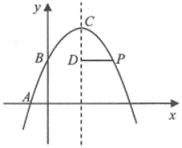
如图，在平面直角坐标系中，抛物线 
与x轴交于A(1，0)，B两点，与y轴交于点C(0，5).
(1)
求抛物线的解析式；
(2)
若点 P 在以点 B 为圆心，2为半径的⊙B上，⊙B与x轴交于 D，E两点(点D在点 E 左侧)，连接AP，以AP 为边在 AP 下方作等腰 Rt△APQ，且. 
连接EQ，求EQ长度的取值范围.
【考点】
待定系数法求二次函数解析式;
点与圆的位置关系;
二次函数图象上点的坐标特征;
三角形全等的判定-SAS;
圆与函数的综合;
