【特例感知】

1. 【特例感知】

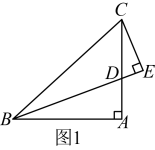
(1) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接CD ，则 $\text{[math]}$ ▲ ；

(2) 【类比迁移】

如图2，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转得到 $\text{[math]}$ ，且满足点B ， C ， E三点共线．若 $\text{[math]}$ ，请猜想BE ， DE ， AE之间具有怎样的数量关系？并说明理由．

(3) 【问题解决】

如图3，某市政府为了提升城市的生态环境质量，促进城市与自然的和谐共生，决定在一块空地上规划公园，其中点 $\text{[math]}$ 为公园入口，点 $\text{[math]}$ ，点 $\text{[math]}$ 是公园出口，入口 $\text{[math]}$ 与出口B ， C的距离相等，且满足 $\text{[math]}$ ，点 $\text{[math]}$ 为公园中的观景点，若 $\text{[math]}$ 米， $\text{[math]}$ 米，计划修建一条观赏栈道BD ，要使得栈道尽可能地长，求四边形ABCD的面积．

【考点】

三角形全等及其性质; 三角形全等的判定; 等边三角形的判定与性质; 旋转的性质; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 已知，在等边三角形 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ．

(1) 【特殊情况，探索结论】如图1，当点 $\text{[math]}$ 为 $\text{[math]}$ 的中点时，确定线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，请你直接写出结论： $\text{[math]}$ $\text{[math]}$ 填“ $\text{[math]}$ ”，“ $\text{[math]}$ ”或“ $\text{[math]}$ ” $\text{[math]}$ ．

(2) 【特例启发，解答题目】如图2，当点 $\text{[math]}$ 为 $\text{[math]}$ 边上任意一点时，请判断线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，并说明理由．

(3) 【拓展结论，设计新题】在等边三角形 $\text{[math]}$ 中，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ，若 $\text{[math]}$ 的边长为3， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．

实践探究题困难

2. 综合与实践

问题情境：

数学活动课上，老师引导学生用一块等腰直角三角板和一个正方形展开探究活动．将正方形的一个顶点与等腰直角三角板的斜边的中点重合，观察不同的摆放方法下其中某些线段之间的数量关系与位置关系．

(1) 知识初探：

将等腰直角三角形 $\text{[math]}$ 与正方形 $\text{[math]}$ 如图 $\text{[math]}$ 摆放，使正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ 与等腰直角三角板斜边 $\text{[math]}$ 的中点 $\text{[math]}$ 重合，且 $\text{[math]}$ 边经过点 $\text{[math]}$ ，请你直接写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系和位置关系．

(2) 类比再探：

如图 $\text{[math]}$ ，正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ 与等腰直角三角板斜边 $\text{[math]}$ 的中点 $\text{[math]}$ 重合， $\text{[math]}$ 边不经过点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，此时 $\text{[math]}$ 与 $\text{[math]}$ 又有怎样的数量关系和位置关系？请说明理由．

(3) 拓展延伸：

如图 $\text{[math]}$ ，正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ 与等腰直角三角板斜边 $\text{[math]}$ 的中点 $\text{[math]}$ 重合，正方形 $\text{[math]}$ 的两条对角线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，取 $\text{[math]}$ 的中点 $\text{[math]}$ ，连接 $\text{[math]}$ ，请你直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系与位置关系．