1.
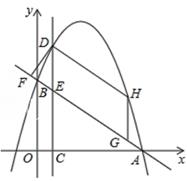
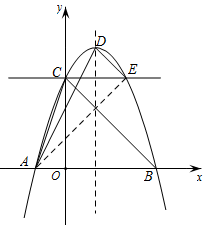
如图1，我们把一个半圆和抛物线的一部分围成的封闭图形称为“果圆” ，已知A，B，C，D分别为“果圆”与坐标轴的交点，y=
x-3与“果圆” 中的抛物线y=
+bx+c交于B，C两点．
(1)
求“果圆”中的抛物线的解析式，并直接写出“果圆”被y轴截得的线段BD的长．
(2)
“果圆”上是否存在点P使∠APC=∠CAB？如果存在请求出点P的坐标；如果不存在，请说明理由．
(3)
如图2，E为直线BC下方“果圆”上一点，连接AE，AB，BE，设AE与BC交于F，△BEF的面积记为S△BEF ， △ABF的面积记为S△ABF ， 求
的最小值．
【考点】
相似三角形的判定与性质;
二次函数的实际应用-几何问题;
