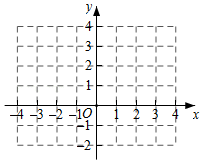1.
在平面直角坐标系xOy中，过点
作垂直于
轴的直线
， 将函数图象位于直线上的点及直线右侧的部分（用
表示）沿翻折，再向左平移
个单位得到新的函数图象
， 我们称这种变换为轴移变换，记作：
． 由与组成的新的图象对应的函数叫做“距美函数”．某学习小组研究直线
经过
得到的“距美函数”，请按照该组同学的探究思路完成以下问题：
首先通过列表、描点、连线的方法作出该函数的图象并对其性质进行了探究．
如表与
的几组对应值：
… | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … | |
… | 3 | 1 | -1 | -1 | 1 | 3 | 5 | 7 | 9 | … |
(1)
如图，根据“轴移变换”的定义，在平面直角坐标系中，描出函数经过轴移变换后各对应值为坐标的点，并根据描出的点，请你画出轴移变化后的函数图象；并观察“距美函数”的图象，当
随的增大而减小时，的取值范围是 ▲ ；
(2)
若
为该函数图象上不同的两点，则
▲ ；
(3)
当距美函数的y值满足：
时，自变量的取值范围是 ▲ ；
(4)
已知点
， 当直线
经过
得到的“距美函数”的图象与线段AB的恰好有1个交点，直接写出k的取值范围 ▲ 。
【考点】
一次函数的图象;
一次函数图象与几何变换;
待定系数法求一次函数解析式;
一次函数的性质;
描点法画函数图象;
能力提升
