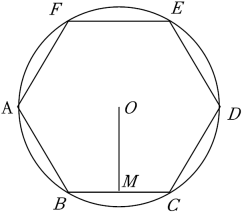
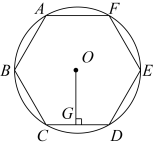
如图，平面直角坐标系中，原点O为正六边形的中心，轴，点E在双曲线（k为常数，）上，将正六边形向上平移个单位长度，点D恰好落在双曲线上，则k的值为．

0 返回出卷网首页

1. 如图，平面直角坐标系中，原点O为正六边形 $\text{[math]}$ 的中心， $\text{[math]}$ 轴，点E在双曲线 $\text{[math]}$ （k为常数， $\text{[math]}$ ）上，将正六边形 $\text{[math]}$ 向上平移 $\text{[math]}$ 个单位长度，点D恰好落在双曲线上，则k的值为．

【考点】

等边三角形的判定与性质; 勾股定理; 圆内接正多边形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 如图，在一个池塘两旁有一条笔直小路（B，C为小路端点）和一棵小树（A为小树位置）测得的相关数据为： $\text{[math]}$ 米，则 $\text{[math]}$ 米.

填空题容易

2. 如图，在△ABC中，AB＝AC，AD是△ABC的一条角平分线，若AB＝13.AD＝12.则BC的长为.

填空题容易

3. 如图，有一块直角三角形纸片，直角边AC＝3cm，BC＝4cm，将直角边AC沿AD所在的直线折叠，使点C落在斜边AB上的点E处，则CD的长为cm．

填空题容易