1.
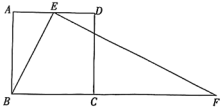
如图,现有正方形纸片 , 点
, 点 ,
,  分别在边
分别在边 ,
,  上,沿垂直于
上,沿垂直于 的直线折叠得到折痕
的直线折叠得到折痕 , 点
, 点 ,
,  分别落在正方形所在平面内的点
分别落在正方形所在平面内的点 ,
,  处,然后还原.
处,然后还原.

(1)
若点 在边
在边 上,且
上,且 , 求
, 求 的大小(用含
的大小(用含 的式子表示);
(2)
再沿垂直于
的式子表示);
(2)
再沿垂直于 的直线折叠得到折痕
的直线折叠得到折痕 , 点
, 点 ,
,  分别在边
分别在边 ,
,  上,点
上,点 落在正方形所在平面内的点
落在正方形所在平面内的点 处,然后还原.若
处,然后还原.若 , 点
, 点 在线段
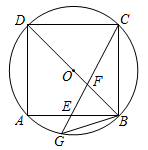
在线段 上,且四边形
上,且四边形 是正方形,
是正方形, 与
与 的交点为
的交点为 ,
,  与
与 的交点为
的交点为 , 连接
, 连接 . 小明同学猜想:
. 小明同学猜想: 的面积是
的面积是 的2倍,他的猜想是否正确?如正确,请给予证明;若不正确,请求出两三角形面积的比
的2倍,他的猜想是否正确?如正确,请给予证明;若不正确,请求出两三角形面积的比 .
.
【考点】
勾股定理;
正方形的性质;
相似三角形的判定与性质;