1.
已知等边 的边长为
的边长为 , 点
, 点 ,
,  分别是直线
分别是直线 ,
,  上的动点.
上的动点.

(1)
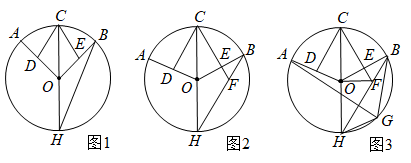
如图1,当点 从顶点
从顶点 沿
沿 向
向 点运动,点
点运动,点 同时从顶点
同时从顶点 沿
沿 向
向 点运动,它们的速度都为
点运动,它们的速度都为 , 连接
, 连接 ,
,  , 设点P运动时间为
, 设点P运动时间为 , (
, ( ).
(2)
当点P在边
).
(2)
当点P在边 , 点Q在直线BC上的运动,且
, 点Q在直线BC上的运动,且 时,请直接写出
时,请直接写出 、
、 和
和 之间的数量关系,不需证明.
之间的数量关系,不需证明.
①用含t的代数式表示长为
;
②当时,求
的度数;
③当t为何值时,是直角三角形?
【考点】
等边三角形的判定与性质;
含30°角的直角三角形;