1.
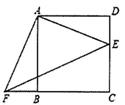
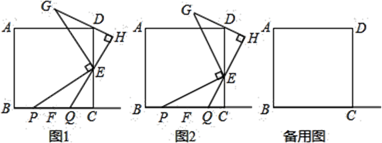
已知：在等边△ABC中， AB= 
，D，E分别是AB，BC的中点（如图1）．若将△BDE绕点B逆时针旋转，得到△BD1E1 ， 设旋转角为α（0°＜α＜180°），记射线CE1与AD1的交点为P．
(1)
判断△BDE的形状；
(2)
在图2中补全图形，
(3)
点P到BC所在直线的距离的最大值为．（直接填写结果）
①猜想在旋转过程中，线段CE1与AD1的数量关系并证明；
②求∠APC的度数；
【考点】
全等三角形的判定与性质;
旋转的性质;
