0 返回出卷网首页
1. 如图，△AOB，△COD是等腰直角三角形，点D在AB上，

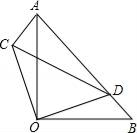
(1) 求证：△AOC≌△BOD；
(2) 若AD=3，BD=1，求CD．
【考点】
全等三角形的判定与性质; 勾股定理; 等腰直角三角形;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 已知△ABC和△ADE是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE中点，连接DF、CF．

(1) 如图1，当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；
(2) 如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；
(3) 如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD=1，AC= ，求此时线段CF的长（直接写出结果）．
综合题 普通
2. 如图，在△ABC中，AB＝AC，点D、E在线段BC上，且BE＝CD，连接AD、AE，过点D作DF⊥AE，垂足为H，交AC于点F，过点E作EG⊥AC，垂足为G．

(1) 若DH＝4，AD＝5，HF＝1，求AF的长；
(2) 若∠BAC＝90°，求证：AF＝2CG．
综合题 普通
3. 已知△ABD与△GDF都是等腰直角三角形，BD与DF均为斜边（BD＜DF）．

(1) 如图1，B，D，F在同一直线上，过F作MF⊥GF于点F，取MF=AB，连结AM交BF于点H，连结GA，GM．

①求证：AH=HM；

②请判断△GAM的形状，并给予证明；

③请用等式表示线段AM，BD，DF的数量关系，并说明理由．
(2) 如图2，GD⊥BD，连结BF，取BF的中点H，连结AH并延长交DF于点M，请用等式直接写出线段AM，BD，DF的数量关系．
综合题 困难