1.
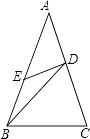
某个零件的的形状如图所示,按规定∠A等于90°,∠B、∠D应分别等于20°和30°,小李量得∠BCD=145°,他断定这个零件不合格,你能说出其中的道理吗?

【考点】
三角形内角和定理;
三角形的外角性质;
能力提升
变式训练
拓展培优
真题演练