如图，点C在⊙O上，连接CO并延长交弦AB于点D，弧AC=弧BC，连接AC、OB，若CD=8，AC= ．

0 返回出卷网首页

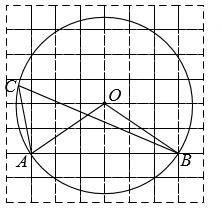
1. 如图，点C在⊙O上，连接CO并延长交弦AB于点D，弧AC=弧BC，连接AC、OB，若CD=8，AC= $\text{[math]}$ ．

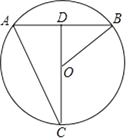
(1) 求弦AB的长；（1）根据垂径定理得出CD⊥AB，AB=2AD=2BD，根据勾股定理算出AD的长，从而得出答案；

(2) 求sin∠ABO的值．

【考点】

勾股定理; 垂径定理; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，已知Rt△ABC中，∠ACB＝90°，cot∠BAC＝2，BC＝4，以边AC上一点O为圆心，OA为半径的⊙O经过点B ．

(1) 求⊙O的半径；

(2) 点P是劣弧 $\text{[math]}$ 的中点，求tan∠PAB的值．

综合题普通

2. 如图，AB为⊙O直径，点D为AB下方⊙O上一点，点C为弧ABD中点，连接CD，CA．

(1) 求证：∠ABD=2∠BDC；

(2) 过点C作CH⊥AB于H，交AD于E，求证：EA=EC；

(3) 在（2）的条件下，若OH=5，AD=24，求线段DE的长

综合题普通

3. 已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．

(1) 求证：AC=BD；

(2) 若大圆的半径R=10，小圆的半径r=8，且圆O到直线AB的距离为6，求AC的长．

综合题普通