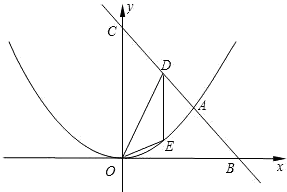
已知：如图，一次函数y=kx﹣1的图象经过点A（3 ，m）（m＞0），与y轴交于点B．点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D．若AC=CD．

0 返回出卷网首页

1. 已知：如图，一次函数y=kx﹣1的图象经过点A（3 $\text{[math]}$ ，m）（m＞0），与y轴交于点B．点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D．若AC=CD．

(1) 求这个一次函数的表达式；

(2) 已知一开口向下、以直线CD为对称轴的抛物线经过点A，它的顶点为P，若过点P且垂直于AP的直线与x轴的交点为Q（﹣ $\text{[math]}$ ，0），求这条抛物线的函数表达式．

【考点】

待定系数法求一次函数解析式; 待定系数法求二次函数解析式; 两条直线被一组平行线所截，所得的对应线段成比例; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

如图1，抛物线C₁： $\text{[math]}$ 与x轴交于A(－1，0)，B(3，0)两点，且顶点为C，直线y=kx+2经过A，C两点．

(1) 求直线AC的表达式与抛物线C₁的表达式；

(2) 如图2，将抛物线C₁沿射线AC方向平移一定距离后，得到抛物线为C₂ ，其顶点为D，抛物线C₂与直线y=kx+2的另一交点为E，与x轴交于M，N两点(M点在N点右边)，若 $\text{[math]}$ ，求点D的坐标；

(3) 如图3，若抛物线C₁向上平移4个单位得到抛物线C₃ ，正方形GHST的顶点G，H在x轴上，顶点S，T在x轴上方的抛物线C₃上，P（m，0）是射线GH上一动点，则正方形GHST的边长为，当m=时， $\text{[math]}$ 有最小值．

综合题困难

2. 如图，二次函数图象的顶点为坐标系原点O ，且经过点 $\text{[math]}$ ，一次函数的图象经过点A和点 $\text{[math]}$ ．

(1) 求二次函数与一次函数的解析式；

(2) 如果一次函数图象与y轴相交于点C ，点D在线段AC上，与y轴平行的直线DE与二次函数图象相交于点E ， $\text{[math]}$ ，求点D的坐标；

(3) 当点D在直线AC上的一个动点时，以点O、C、D、E为顶点的四边形能成为平行四边形吗？请说明理由．

综合题普通

3. 如图，在平面直角坐标系xOy中，直线 $\text{[math]}$ 与x轴、y轴分别交于点A、B．抛物线 $\text{[math]}$ （a≠0）经过点A，且与y轴相交于点C，∠OCA=∠OAB．

(1) 求直线AB的表达式；

(2) 如果点D在线段AB的延长线上，且AD=AC．求经过点D的抛物线 $\text{[math]}$ 的表达式；

(3) 如果抛物线 $\text{[math]}$ 的对称轴与线段AB、AC分别相交于点E、F，且EF=1，求此抛物线的顶点坐标．

综合题普通