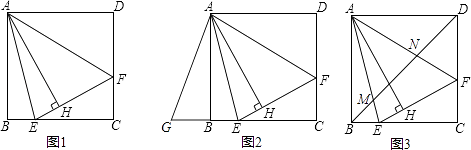
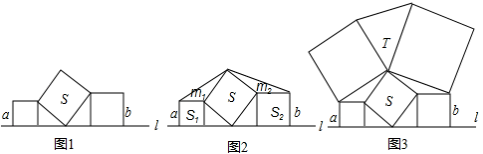
1.
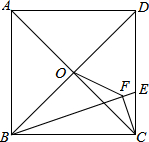
如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,若DN=1,BM=2,那么MN=.证明:DN2+BM2=MN2 .
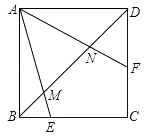
【考点】
全等三角形的判定与性质;
勾股定理的应用;
正方形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练