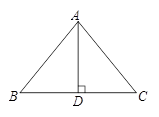
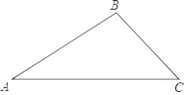
如图，有一个三角形的钢架ABC，∠A=30°，∠C=45°，AC=2（ +1）m．请计算说明，工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门？

0 返回出卷网首页

1. 如图，有一个三角形的钢架ABC，∠A=30°，∠C=45°，AC=2（ $\text{[math]}$ +1）m．请计算说明，工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门？

【考点】

解直角三角形; 解直角三角形的其他实际应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 我们把底角为51°的等腰三角形称为最稳定三角形. 如图，已知△ABC是最稳定三角形， AB=AC，BC=232.8m.求BC边上的高AD的长.

（sin51°≈0.8，cos51°≈0.6，tan51°≈1.2，精确到1m）

解答题容易

2. 某超大型集装箱船，船身呈长方形，如图所示，长 $\text{[math]}$ 米，宽 $\text{[math]}$ 米，船身和河岸的夹角 $\text{[math]}$ ．河岸 $\text{[math]}$ ，求河岸 $\text{[math]}$ 与 $\text{[math]}$ 之间的距离（结果保留根号）．

解答题容易

3. “醒狮”是岭南文化名城佛山一块闪亮的招牌，是国家非物质文化遗产之一．舞狮者用狮嘴将悬于高处、寓意着吉祥的“生菜”采摘的过程称为“采青”．舞狮者脚站立的位置与狮嘴可触摸到的位置之间的距离称为“采摘距离”．如图，舞狮者站在梅花桩AB上，AB与“生菜”放置点D的水平距离BC为1.1米，LD=53°．已知该舞狮者采摘距离为1.43米，请利用所学知识判断该舞狮者能否“采青”成功，并说明理由．

（参考数据：sin53°~0.8，cos53°~0.6，tan53~1.3）

解答题容易