1.
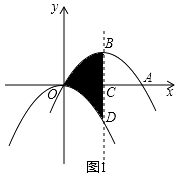
如图1,抛物线  平移后过点A(8,0)和原点,顶点为B,对称轴与
平移后过点A(8,0)和原点,顶点为B,对称轴与  轴相交于点C,与原抛物线相交于点D.
轴相交于点C,与原抛物线相交于点D.

(1)
求平移后抛物线的解析式并直接写出阴影部分的面积  ;
(2)
如图2,直线AB与
;
(2)
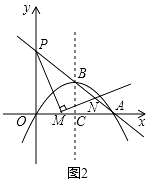
如图2,直线AB与  轴相交于点P,点M为线段OA上一动点,
轴相交于点P,点M为线段OA上一动点,  为直角,边MN与AP相交于点N,设
为直角,边MN与AP相交于点N,设  ,试探求:
,试探求:
① 为何值时
为等腰三角形;
② ![]() 为何值时线段PN的长度最小,最小长度是多少.
为何值时线段PN的长度最小,最小长度是多少.
【考点】
二次函数图象的几何变换;
相似三角形的判定与性质;
二次函数与一元二次方程的综合应用;
能力提升


