1.
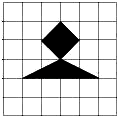
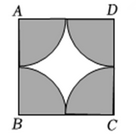
如图,在正方形 中,分别以四个顶点为圆心,以边长的一半为半径画圆弧,若随机向正方形
中,分别以四个顶点为圆心,以边长的一半为半径画圆弧,若随机向正方形 内投一粒米
内投一粒米 米粒大小忽略不计
米粒大小忽略不计 , 则米粒落在图中阴影部分的概率为.
, 则米粒落在图中阴影部分的概率为.
【考点】
几何概率;
基础巩固
能力提升
变式训练
拓展培优
真题演练