在平行四边形ABCD中，E为AB的中点，F为BC上一点．

0 返回出卷网首页

1. 在平行四边形ABCD中，E为AB的中点，F为BC上一点．

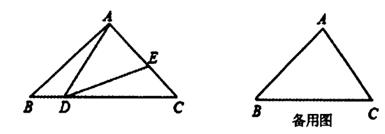
(1) 如图1，若AF⊥BC，垂足为F，BF＝3，AF＝4，求EF的长．

(2) 如图2，若DE和AF相交于点P，点Q在线段DE上，且AQ∥PC，求证：PC＝2AQ．

【考点】

相似三角形的判定与性质; 直角三角形斜边上的中线;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在△ABC和△ADE中，∠DAB＝∠EAC，∠C＝∠E.

(1) 求证：AD·BC＝AB·DE；

(2) 若 $\text{[math]}$ 求DE的长.

综合题普通

2. 如图，在△ABC中，点D、E分别在边BC、AC上，连接AD、DE，且∠B=∠ADE=∠C。

(1) 证明：△BDA∽△CED；

(2) 若∠B=45°，BC=6，当点D在BC上运动时(点D不与B、C重合)。且△ADE是等腰三角形，求此时BD的长。

综合题困难

3. 如图，在 $\text{[math]}$ 中，直线DF与边AB相交于点D，与边AC相交于点E，与线段BC延长线相交于点F.

(1) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，其中m＞n＞0，求 $\text{[math]}$ 的值.

(3) 请根据上述（1）（2）的结论，猜想 $\text{[math]}$ =（直接写出答案，不需要证明）.

综合题困难