0 返回出卷网首页
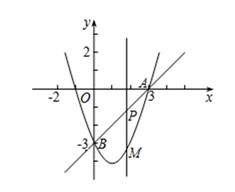
1. 如图，在平面直角坐标系中，抛物线y=x2+mx+n经过点A（3，0）、B（0，-3），点P是直线AB上的动点，过点P作x轴的垂线交抛物线于点M ， 设点P的横坐标为t ．

(1) 分别求出直线AB和这条抛物线的解析式．
(2) 若点P在第四象限，连接AM、BM ， 当线段PM最长时，求△ABM的面积．
(3) 是否存在这样的点P ， 使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由．
【考点】
待定系数法求二次函数解析式; 二次函数-动态几何问题; 二次函数y=ax²+bx+c的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
解答题 困难
能力提升
真题演练
换一批
1.

定义：如图1，抛物线 与 轴交于A，B两点，点P在抛物线上（点P与A，B两点不重合），如果△ABP的三边满足 ，则称点P为抛物线 的勾股点。

(1) 直接写出抛物线 的勾股点的坐标；
(2) 如图2，已知抛物线C： 与 轴交于A，B两点，点P（1， ）是抛物线C的勾股点，求抛物线C的函数表达式；
(3) 在（2）的条件下，点Q在抛物线C上，求满足条件 的点Q（异于点P）的坐标
解答题 困难
2. 在平面直角坐标系中，抛物线 经过点(4，2).点 P 在这条抛物线上，且点 P 的横坐标为m，过点 P 作 PQ⊥y轴，点 Q 的横坐标为2-4m.
(1) 求该抛物线所对应的函数表达式及顶点坐标.
(2) 作以 P 为圆心、半径长为3的⊙P，当⊙P与x轴相切时，求点 P 的坐标.
(3) 当线段 PQ被抛物线分成1：2 两部分时，求 m的值.
(4) 过点 P 作 轴，点 M 的纵坐标为m+2，且点 M 与点 P 不重合，连结 MQ，当抛物线在△PQM内的部分对应的函数值y随x 的增大而减小时，直接写出m的取值范围.
解答题 困难
3. 如图，已知抛物线y=ax2+bx+1经过点（2，6），且与直线 相交于A，B两点，点A在y轴上，过点B作BC⊥x轴，垂足为点C（4，0）．

(1) 求抛物线的解析式；
(2) 若P是直线AB上方该抛物线上的一个动点，过点P作PD⊥x轴于点D，交AB于点E，求线段PE的最大值；
(3) 在（2）的条件，设PC与AB相交于点Q，当线段PC与BE相互平分时，请求出点Q的坐标．
解答题 普通