1.
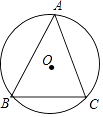
如图,  中,
中,  =90°,
=90°,  平分
平分  交
交  于点
于点  ,
,  是
是  上一点,经过
上一点,经过  、
、  两点的
两点的  分别交
分别交  、
、  于点
于点  、
、  ,
,  ,
,  =60°,则劣弧
=60°,则劣弧  的长为
的长为
【考点】
圆周角定理;
弧长的计算;
解直角三角形;
基础巩固
能力提升
变式训练
拓展培优