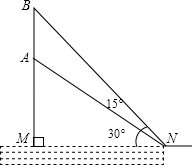
1.
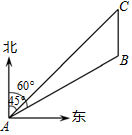
如图所示,巡逻船在A处测得灯塔C在北偏东  方向上,距离A处30km.在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救.已知B处在A处的北偏东
方向上,距离A处30km.在灯塔C的正南方向B处有一渔船发出求救信号,巡逻船接到指示后立即前往施救.已知B处在A处的北偏东  方向上,这时巡逻船与渔船的距离是多少?(精确到0.01km.参考数据:
方向上,这时巡逻船与渔船的距离是多少?(精确到0.01km.参考数据:  ,
,  ,
,  )
)
【考点】
直角三角形的性质;