1.
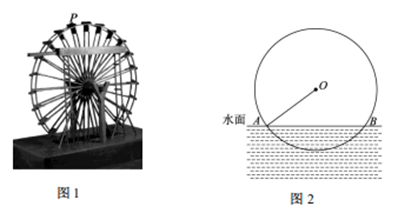
在汽车车轮修理厂,工人师傅常用两个棱长为a的正方形卡住车轮.如图是其截面图(a小于车轮半径),量出两个正方形的距离AB的长为2b,就可以得出车轮的直径.请你推求出直径d的公式.

【考点】
勾股定理;
垂径定理;
切线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练