1.
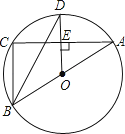
如图,在△ACD中,DA=DC,点B是AC边上一点,以AB为直径的⊙O经过点D,点F是直径AB上一点(不与A、B重合),延长DF交圆于点E,连结EB.

(1)
求证:∠C=∠E;
(2)
若弧AE=弧BE,∠C=30°,DF=  ,求AD的长.
,求AD的长.
【考点】
含30°角的直角三角形;
垂径定理;
圆周角定理;