1.
如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱ALMN,若中间空白部分四边形OPQR恰好是正方形,且▱ALMN的面积为50,则正方形EFGH的面积为( )
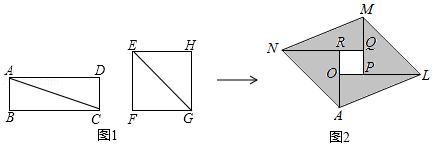
A.
24
B.
25
C.
26
D.
27
【考点】
矩形的性质;
正方形的性质;