1.
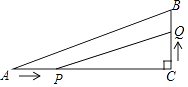
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.

(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.

(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.
【考点】
二次函数的最值;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练