1.
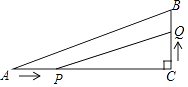
如图 , 在
, 在 中,
中, ,
,  , 动点
, 动点 从点
从点 开始沿
开始沿 边以每秒
边以每秒 个单位长度的速度运动,同时,动点
个单位长度的速度运动,同时,动点 从点
从点 开始沿
开始沿 边以相同速度运动,当其中一点停止运动时,另一点同时停止运动,连接
边以相同速度运动,当其中一点停止运动时,另一点同时停止运动,连接 ,
,  为
为 中点,连接
中点,连接 ,
,  , 设时间为
, 设时间为 ,
,  为
为 ,
,  关于
关于 的函数图象如图
的函数图象如图 所示,则下列说法正确的是( )
所示,则下列说法正确的是( )
当
时,
;
;
有最小值,最小值为
;
有最小值,最小值为
.

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
二次函数的最值;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练