1.
在平面直角坐标系中,点  是原点,四边形
是原点,四边形  是矩形,点
是矩形,点  ,点
,点  .以点
.以点  为中心,顺时针旋转矩形
为中心,顺时针旋转矩形  ,得到矩形
,得到矩形  ,点
,点  的对应点分别为
的对应点分别为  .
.


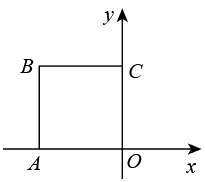
(1)
如图①,当点  落在
落在  边上时,求点
边上时,求点  的坐标;
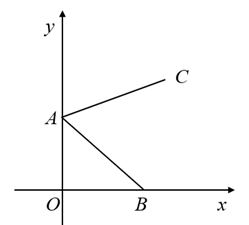
(2)
如图②,当点
的坐标;
(2)
如图②,当点  落在线段
落在线段  上时,
上时,  与
与  交于点
交于点  .求点
.求点  的坐标;
(3)
记
的坐标;
(3)
记  为矩形
为矩形  对角线的交点,
对角线的交点,  为
为  的面积,求
的面积,求  的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
【考点】
坐标与图形性质;
旋转的性质;
能力提升
真题演练