1.
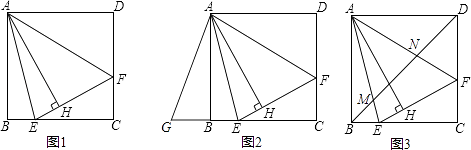
问题：如图1，在正方形ABCD内有一点P，PA= 
，PB= 
，PC=1，求∠BPC的度数．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．
，PB= ，PC=1，求∠BPC的度数．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′． 
请你参考小明同学的思路，解决下列问题：
(1)
图2中∠BPC的度数为；
(2)
如图3，若在正六边形ABCDEF内有一点P，且PA= 
，PB=4，PC=2，则∠BPC的度数为，正六边形ABCDEF的边长为．
【考点】
正方形的性质;
旋转的性质;
