1.
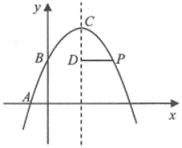
在平面直角坐标系xOy中，抛物线 
与x轴交于 
，点 
两点，与y轴交于点C
(1)
求抛物线的解析式：
(2)
若点P是抛物线上在第二象限内的一个动点，且点P的横坐标为t，连接PA、PC、AC．
求
的面积S关于t的函数关系式．
求
的面积的最大值，并求出此时点P的坐标．
【考点】
待定系数法求二次函数解析式;
二次函数图象上点的坐标特征;
二次函数y=a（x-h）²+k的性质;
