1.
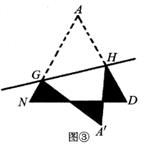
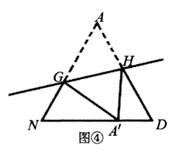
如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是(写出所有符合题意结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF= ;
③当A、F、C三点共线时,AE= ;
④当A、F、C三点共线时,△CEF≌△AEF .

【考点】
全等三角形的判定与性质;
翻折变换(折叠问题);
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练