1.
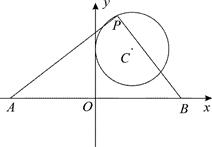
如图,直线y=x+b(b>0)与x、y轴分别相交于A、B两点,点C(1,0),过点C作垂直于x轴的直线l,在直线l上取一点P,满足PA=PB,点A关于直线l的对称点为点D,以D为圆心,DP为半径作⊙D.
(1)直接写出点A、D的坐标;(用含b的式子表示)
(2)求点P的坐标;
(3)试说明:直线BP与⊙D相切.

【考点】
勾股定理;
圆的综合题;