1.
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为这边上的“奇特三角形”,这条边称为“奇特边”.
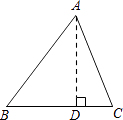
(1)如图1,已知△ABC是奇特三角形, , 且∠C=90°.
①△ABC的奇特边是 ;
②设 ,
,
, 求a:b:c;
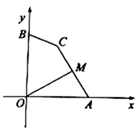
(2)如图2,AM是△ABC的中线,若△ABC是BC边上的奇特三角形,找出BC2与AB2+AC2之间的关系;
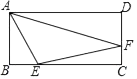
(3)如图3,在四边形ABCD中,∠B=90°(AB<BC), , 对角线AC把它分成了两个奇特三角形,且△ACD是以AC为腰的等腰三角形,求等腰△ACD的底边长.

【考点】
勾股定理;
能力提升
变式训练
拓展培优
真题演练