1.
如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
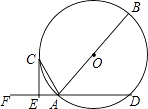
(1)
求证:CE是⊙O的切线;
(2)
若AE=1,CE=2,求⊙O的半径.
【考点】
角平分线的性质;
切线的判定;