1.
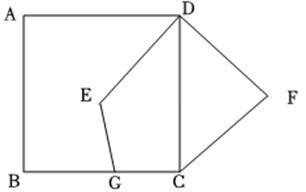
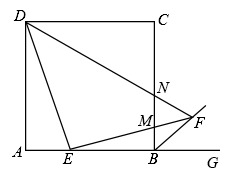
如图,四边形ABCD、EFGH、NHMC都是正方形,边长分别为a,b,c;A,B,N,E,F五点在同一直线上,则c=(用含有a,b的代数式表示).

【考点】
三角形全等的判定;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练