如图，矩形OABC的两边在坐标轴上，连接AC，抛物线y=x2﹣4x﹣2经过A，B两点．

0 返回出卷网首页

1. 如图，矩形OABC的两边在坐标轴上，连接AC，抛物线y=x²﹣4x﹣2经过A，B两点．

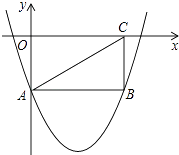
(1) 求A点坐标及线段AB的长；

(2) 若点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿AO，OC，CB边向点B移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒．

①当PQ⊥AC时，求t的值；

②当PQ∥AC时，对于抛物线对称轴上一点H，∠HOQ＞∠POQ，求点H的纵坐标的取值范围．

【考点】

待定系数法求一次函数解析式; 二次函数图象与坐标轴的交点问题; 勾股定理; 相似三角形的判定与性质; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知二次函数的图象经过A（2，0）、C（0，12）两点，且对称轴为直线x=4．设顶点为点P，与x轴的另一交点为点B．

(1) 求二次函数的解析式及顶点P的坐标；

(2) 如图1，在直线 y=2x上是否存在点D，使四边形OPBD为等腰梯形？若存在，求出点D的坐标；若不存在，请说明理由；

(3) 如图2，点M是线段OP上的一个动点（O、P两点除外），以每秒 $\text{[math]}$ 个单位长度的速度由点P向点O 运动，过点M作直线MN∥x轴，交PB于点N．将△PMN沿直线MN对折，得到△P₁MN．在动点M的运动过程中，设△P₁MN与梯形OMNB的重叠部分的面积为S，运动时间为t秒．求S关于t的函数关系式．

综合题困难

2. 已知，抛物线y＝mx²＋ $\text{[math]}$ x﹣4m与x轴交于点A（﹣4，0）和点B ，与y轴交于点C ．点D（n ， 0）为x轴上一动点，且有﹣4＜n＜0，过点D作直线1⊥x轴，且与直线AC交于点M ，与抛物线交于点N ，过点N作NP⊥AC于点P ．点E在第三象限内，且有OE＝OD ．

(1) 求m的值和直线AC的解析式．

(2) 若点D在运动过程中， $\text{[math]}$ AD＋CD取得最小值时，求此时n的值．

(3) 若点△ADM的周长与△MNP的周长的比为5∶6时，求AE＋ $\text{[math]}$ CE的最小值．

综合题困难

3. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接 $\text{[math]}$ ．

(1) 求线段AC的长；

(2) 若点Р为该抛物线对称轴上的一个动点，当 $\text{[math]}$ 时，求点P的坐标；

(3) 若点M为该抛物线上的一个动点，当 $\text{[math]}$ 为直角三角形时，求点M的坐标．

综合题困难