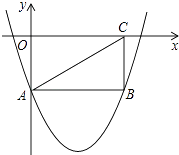
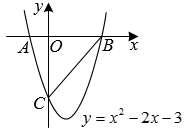
如图，在平面直角坐标系中，抛物线与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接．

0 返回出卷网首页

1. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接 $\text{[math]}$ ．

(1) 求线段AC的长；

(2) 若点Р为该抛物线对称轴上的一个动点，当 $\text{[math]}$ 时，求点P的坐标；

(3) 若点M为该抛物线上的一个动点，当 $\text{[math]}$ 为直角三角形时，求点M的坐标．

【考点】

二次函数图象与坐标轴的交点问题; 勾股定理; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．

(1) 求抛物线的解析式及点C的坐标；

(2) 求证：△ABC是直角三角形；

(3) 若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．

综合题普通

2. 平面直角坐标系中，抛物线 $\text{[math]}$ 与y轴交于点A．

(1) 求点A的坐标及抛物线的对称轴；

(2) 若 $\text{[math]}$ ， y有最大值为3，求a的值；

(3) 已知点 $\text{[math]}$ 、 $\text{[math]}$ ，若线段 $\text{[math]}$ 与抛物线只有一个公共点，结合函数图象，求a的取值范围．

综合题困难

3. 如图，抛物线y＝x²﹣ $\text{[math]}$ x﹣4与x轴相交于A、B两点（点A在点B的左侧），与y轴交于点C，顶点为 D.

(1) 求出A、B两点的坐标；

(2) 连接AC，点P为第四象限抛物线上的一个动点，P的坐标为P（t，p），四边形ACPB面积为S，求S与t的函数关系式，并求t为何值时，S最大？

(3) 在（2）的基础上，若点M为抛物线上的一个动点，在抛物线对称轴上是否存在这样的点N，使以A、M、P、N为顶点的四边形是平行四边形？如果存在，直接写出满足条件的M，N点的坐标；如果不存在，请说明理由.

综合题困难