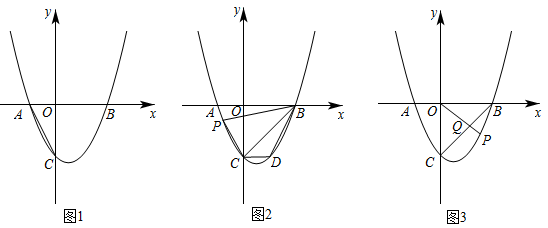
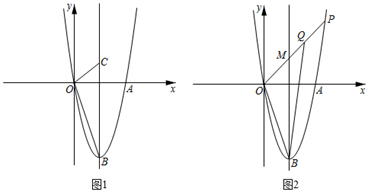
如图1，已知直线y=kx与抛物线y= 交于点A（3，6）．

0 返回出卷网首页

1. 如图1，已知直线y=kx与抛物线y= $\text{[math]}$ 交于点A（3，6）．

(1) 求直线y=kx的解析式和线段OA的长度；

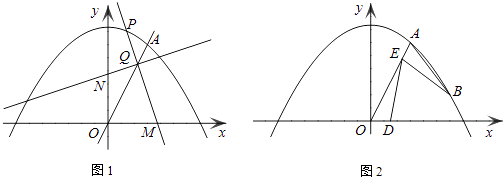
(2) 点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；

(3) 如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？

【考点】

相似三角形的判定与性质; 锐角三角函数的定义; 二次函数与一次函数的综合应用; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1，已知二次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ 、 $\text{[math]}$ ，与y轴交于点C，且 $\text{[math]}$ .

(1) 求二次函数的解析式；

(2) 如图2，过点C作 $\text{[math]}$ 轴交二次函数图象于点D，P是二次函数图象上异于点D的一个动点，连接PB、PC，若 $\text{[math]}$ ，求点P的坐标；

(3) 如图3，若点P是二次函数图象上位于BC下方的一个动点，连接OP交BC于点Q.设点P的横坐标为t，试用含t的代数式表示 $\text{[math]}$ 的值，并求 $\text{[math]}$ 的最大值.

综合题困难

2. 在平面直角坐标系xOy中，二次函数y＝ax²+bx的图象与x轴交于O、A两点，其顶点B的坐标为（2，﹣6）.

(1) 求a、b的值；

(2) 如图1，点C是该二次函数图象的对称轴上的一个动点，连接BO、CO，当△OBC是以BC为腰的等腰三角形时，求点C的坐标；

(3) 如图2，P是该二次函数图象上的位于第一象限内的一个动点，连接OP，与对称轴交于点M，点Q在OP上，满足 $\text{[math]}$ ＝ $\text{[math]}$ ，设点P的横坐标为n；

①请用含n的代数式表示点Q的坐标（，）；

②连接BQ，OB，当△OBQ的面积为15时，求点P的坐标；

③当∠POA＝2∠OBM时，直接写出点P的横坐标.

综合题困难

3. 如图，在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），与 $\text{[math]}$ 轴交于 $\text{[math]}$ 点，经过点 $\text{[math]}$ 的直线 $\text{[math]}$ ： $\text{[math]}$ 与 $\text{[math]}$ 轴负半轴交于点 $\text{[math]}$ ，与抛物线的另一个交点为 $\text{[math]}$ ，且 $\text{[math]}$ .

(1) 直接写出点 $\text{[math]}$ 的坐标，并求直线 $\text{[math]}$ 的函数表达式（其中 $\text{[math]}$ 、 $\text{[math]}$ 用含 $\text{[math]}$ 的式子表示）；

(2) 是否存在 $\text{[math]}$ 和相应的 $\text{[math]}$ 轴正半轴上一点 $\text{[math]}$ ，使得 $\text{[math]}$ 与 $\text{[math]}$ 相似，如果存在，求出所有 $\text{[math]}$ 的值和点 $\text{[math]}$ 的坐标；若不存在，请说明理由.

综合题困难