1.
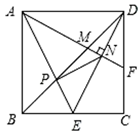
如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=  ;④
;④  ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
A.
1个
B.
2个
C.
3个
D.
4个
【考点】
勾股定理;
正方形的性质;
两条直线被一组平行线所截,所得的对应线段成比例;
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练