0 返回出卷网首页
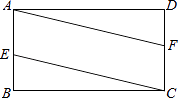
1. 已知四边形ABCD是正方形，点P在直线BC上，点G在直线AD上（P，G不与正方形顶点重合，且在CD的同侧），PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连结EF．

(1) 如图1，当点P与点G分别在线段BC与线段AD上时．

①请直接写出线段DG与PC的数量关系(不要求证明）；

②求证：四边形PEFD是菱形；
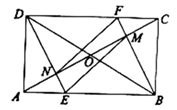
(2) 如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．
【考点】
全等三角形的判定与性质; 平行四边形的判定; 菱形的判定; 矩形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．

(1) 求证：△BEC≌△DFA；
(2) 求证：四边形AECF是平行四边形．
综合题 普通
2. 如图1，在矩形ABCD中，AB=4，AD=5，E为射线BC上一点，DF⊥AE于F，连结DE．

(1) 当E在线段BC上时

①若DE=5，求BE的长；

②若CE=EF，求证：AD=AE；
(2) 连结BF，在点E的运动过程中：

①当△ABF是以AB为底的等腰三角形时，求BE的长；

②记△ADF的面积为S1 ， 记△DCE的面积为S2 ， 当BF∥DE时，请直接写出S1：S2的值．
综合题 普通
3. 如图，在△ABC和△DCB中，AB=DC，AC=DB，AC与DB交于点M．

(1) 求证：△ABC≌△DCB；
(2) 过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断线段BN与CN的数量关系，并证明你的结论．
综合题 普通