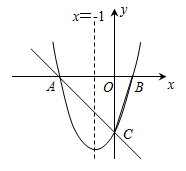1.
在平面直角坐标系  中,抛物线C:
中,抛物线C:  的对称轴是y轴,过点
的对称轴是y轴,过点  作一直线与抛物线C相交于P,Q两点,过点Q作x轴的垂线与直线
作一直线与抛物线C相交于P,Q两点,过点Q作x轴的垂线与直线  相交于点A.
相交于点A.
(1)
求抛物线C的解析式;
(2)
判断点A是否在直线  上,并说明理由;
(3)
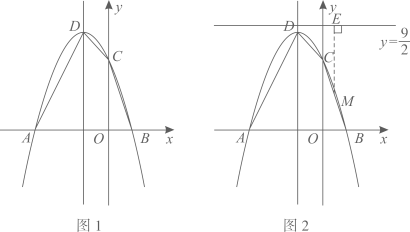
若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切.过抛物线C上的任意一点(除顶点外)作该抛物线的切线l,分别交直线
上,并说明理由;
(3)
若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切.过抛物线C上的任意一点(除顶点外)作该抛物线的切线l,分别交直线  和直线
和直线  于点M,N,求
于点M,N,求  的值.
的值.
【考点】
勾股定理;
二次函数y=ax²+bx+c的图象;
二次函数y=ax²+bx+c的性质;
能力提升
真题演练