1.
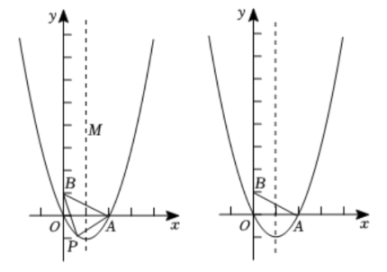
已知抛物线 与x轴交于点
与x轴交于点 , 顶点为B.
, 顶点为B.
(1)
 时,
时, 时,求抛物线的顶点B的坐标;
(2)
求抛物线
时,求抛物线的顶点B的坐标;
(2)
求抛物线 与
与 轴的另一个公共点的坐标
轴的另一个公共点的坐标 用含a,c的式子表示
用含a,c的式子表示 ;
(3)
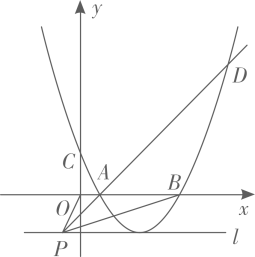
若直线
;
(3)
若直线 经过点B且与抛物线
经过点B且与抛物线 交于另一点
交于另一点 , 求当
, 求当 时,
时, 的取值范围.
的取值范围.
【考点】
待定系数法求二次函数解析式;
二次函数图象与坐标轴的交点问题;
二次函数y=ax²+bx+c的性质;