1.
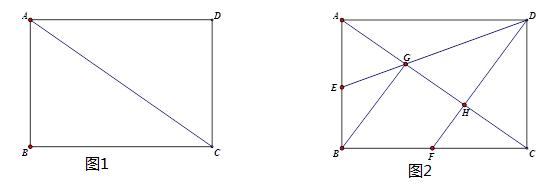
如图,在矩形  中,
中,  ,点E是边
,点E是边  的中点,
的中点,  和
和  的延长线交于点F,点G是边
的延长线交于点F,点G是边  上的一点,且满足
上的一点,且满足  ,连接
,连接  ,
,  ,且
,且  与
与  交于点O.
交于点O.
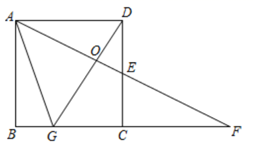
(1)
若  ,求
,求  的面积
(2)
当
的面积
(2)
当  是直角三角形时,求所有满足要求的a值.
(3)
记
是直角三角形时,求所有满足要求的a值.
(3)
记  ,
,  ,
,
①求y关于x的函数关系.
②当 时,求
的值.
【考点】
矩形的性质;
相似三角形的判定与性质;
锐角三角函数的定义;
能力提升
真题演练