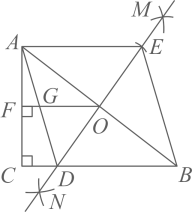
1.
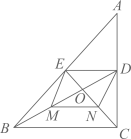
如图,在  中,
中,  分别是边
分别是边  上的中线,
上的中线,  于点O,点
于点O,点  分别是
分别是  的中点,若
的中点,若  ,
,  ,则四边形
,则四边形  的周长是( )
的周长是( )
A.
14
B.
20
C.
22
D.
28
【考点】
菱形的判定与性质;
三角形的中位线定理;



 平行四边形
平行四边形 菱形
菱形 直角梯形
直角梯形