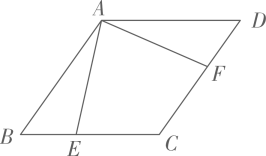
如图，在菱形ABCD中，AB=AC=1，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，连接DH交AC于点O，则下列结论：①△ABF≌△CAE；②∠FHC=∠B；③△ADO≌△ACH；④ ；其中正确的结论个数是（）

1. 如图，桌面上竖直放置一等腰直角三角板 $\text{[math]}$ ，若测得斜边 $\text{[math]}$ 的两端点到桌面的距离分别为 $\text{[math]}$ ， $\text{[math]}$ ．已知 $\text{[math]}$ ， $\text{[math]}$ ，则点 $\text{[math]}$ 距离桌面的高度 $\text{[math]}$ 为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 如图，四边形 $\text{[math]}$ 是菱形，点 $\text{[math]}$ 、 $\text{[math]}$ 分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，点E，F在菱形ABCD的对角线AC上，∠ADC＝120°，∠BEC＝∠CBF＝50°，ED与BF的延长线交于点M．

则对于以下结论：

①∠BME＝30°；

②△ADE≌△ABE；

③EM＝BC．

其中正确结论的个数是（）

A. 0个 B. 1个 C. 2个 D. 3个

单选题容易

1. 如图所示，在平行四边形ABCD中，分别以AB、AD为边作等边△ABE和等边△ADF，分别连接CE，CF和EF，则下列结论，一定成立的个数是（　　）

①△CDF≌△EBC；

②△CEF是等边三角形；

③∠CDF＝∠EAF；

④CE∥DF

A. 1 B. 2 C. 3 D. 4

单选题普通

2. 全等三角形是( )

A. 三个角对应相等的三角形 B. 周长相等的两个三角形 C. 面

积相等的两个三角形 D. 三边对应相等的两个三角形

单选题普通

3. 如图， $\text{[math]}$ 是线段 $\text{[math]}$ 的垂直平分线，垂足为点G，E，F是 $\text{[math]}$ 上两点．下列结论错误的是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

1. 如图，菱形ABCD中，点E、F分别是BC、CD边的中点．求证：AE＝AF ．

证明题普通

2. 如图，在菱形ABCD中，点E是AB上的一点，连结DE交AC于点O，连结BO，且∠AED＝50°，则∠CBO＝度．

填空题普通

3. 已知：如图， $\text{[math]}$ ， $\text{[math]}$ ，请你再添加一个条件，使得 $\text{[math]}$ ，这个条件可以是（只需写出一个即可）．

填空题容易

1. 如图1，在矩形ABCD中，点E，F分别在AB，BC边上，DE=AF，DE⊥AF于点G.

(1) 求证：四边形ABCD是正方形；

(2) 延长CB到点H，使得BH=AE，判断AAHF的形状，并说明理由

(3) 如图2，在菱形ABCD中，点E，F分别在AB，BC边上，DE与AF相交于点G，DE=AF，∠AED=60°，AE=6，BF=2，求DE的长

综合题困难

2. 【问题呈现】

如图1， $\text{[math]}$ 的顶点在正方形 $\text{[math]}$ 两条对角线的交点处， $\text{[math]}$ ，将 $\text{[math]}$ 绕点P旋转，旋转过程中， $\text{[math]}$ 的两边分别与正方形 $\text{[math]}$ 的边 $\text{[math]}$ 和 $\text{[math]}$ 交于点E、F（点F与点C ， D不重合）。探索线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系。

(1) 【问题初探】

爱动脑筋的小悦发现，通过证明两个三角形全等，可以得到结论．请你写出线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由；

(2) 【问题引申】

如图2，将图1中的正方形 $\text{[math]}$ 改为 $\text{[math]}$ 的菱形， $\text{[math]}$ ，其他条件不变，请你帮小悦得出此时线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系是；