1.
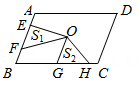
如图,点O是 的对称中心,
的对称中心, ,E、F是
,E、F是 边上的点,且
边上的点,且 ;G、H是
;G、H是 边上的点,且
边上的点,且 ,若
,若 分别表示
分别表示 和
和 的面积,则
的面积,则 与
与 之间的等量关系是( )
之间的等量关系是( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
三角形的面积;
平行四边形的性质;