1.
已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
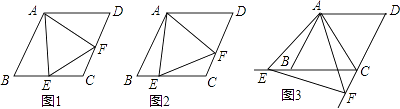
(1)
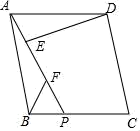
如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)
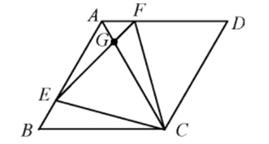
如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)
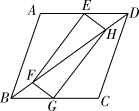
如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
【考点】
全等三角形的判定与性质;
菱形的性质;