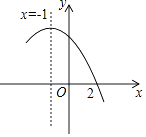1.
如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论:
①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,其中正确的是(填序号).

【考点】
二次函数图象与系数的关系;
二次函数图象的几何变换;
二次函数图象与坐标轴的交点问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练