1.
我们定义：对角线互相垂直的四边形叫做“对垂四边形”。
(1)
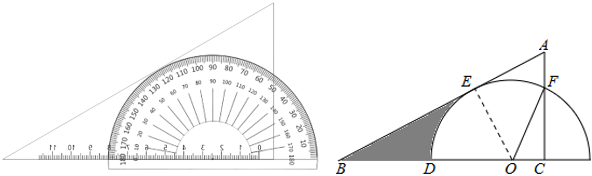
如图1，四边形ABCD为“对垂四边形”。求证：AB²+CD2=BC2+AD²
(2)
如图2，E是四边形ABCD内一点，连结AE，BE，CE和DE，AC与BD交于点O。若∠BEC=90°，∠BAC=∠BDC，∠1+∠2=∠3。求证：四边形ABCD为“对垂四边形”。
(3)
如图3，四边形ABCD为“对垂四边形”，AB=AC，∠ADC=120°，AD=3，BC= 
DC。求CD的长。
【考点】
含30°角的直角三角形;
勾股定理;
